Von Neumann realized that poker was not guided by probability theory alone, as an unfortunate player who would use only probability theory would find out. Von Neumann wanted to formalize the idea of 'bluffing,' a strategy that is meant to deceive the other players and hide information from them. The odds are 1:626 and probability is 0.16%. If you’re playing poker long enough you will somewhat regularly encounter the aces vs. Kings scenario at a table. A formula to estimate the probability for this to happen at a 9 player table is. This formula slightly underestimates the actual probability which is a little bit higher.

1. Probability Theory Probability
2. Probability Theory Predicts That There Is
3. Probability Theory Power System Reliability

Intro

Probability and gambling have been an idea since long before the invention of poker. The development of probability theory in the late 1400s was attributed to gambling; when playing a game with high stakes, players wanted to know what the chance of winning would be. Dutch gives a brief and light history of probability theory, talking about the contributions of Pascal, Laplace, Fermat, and Bayes. Poker Clinic #3 - Probability Theory, Bayes' Theorem and the.

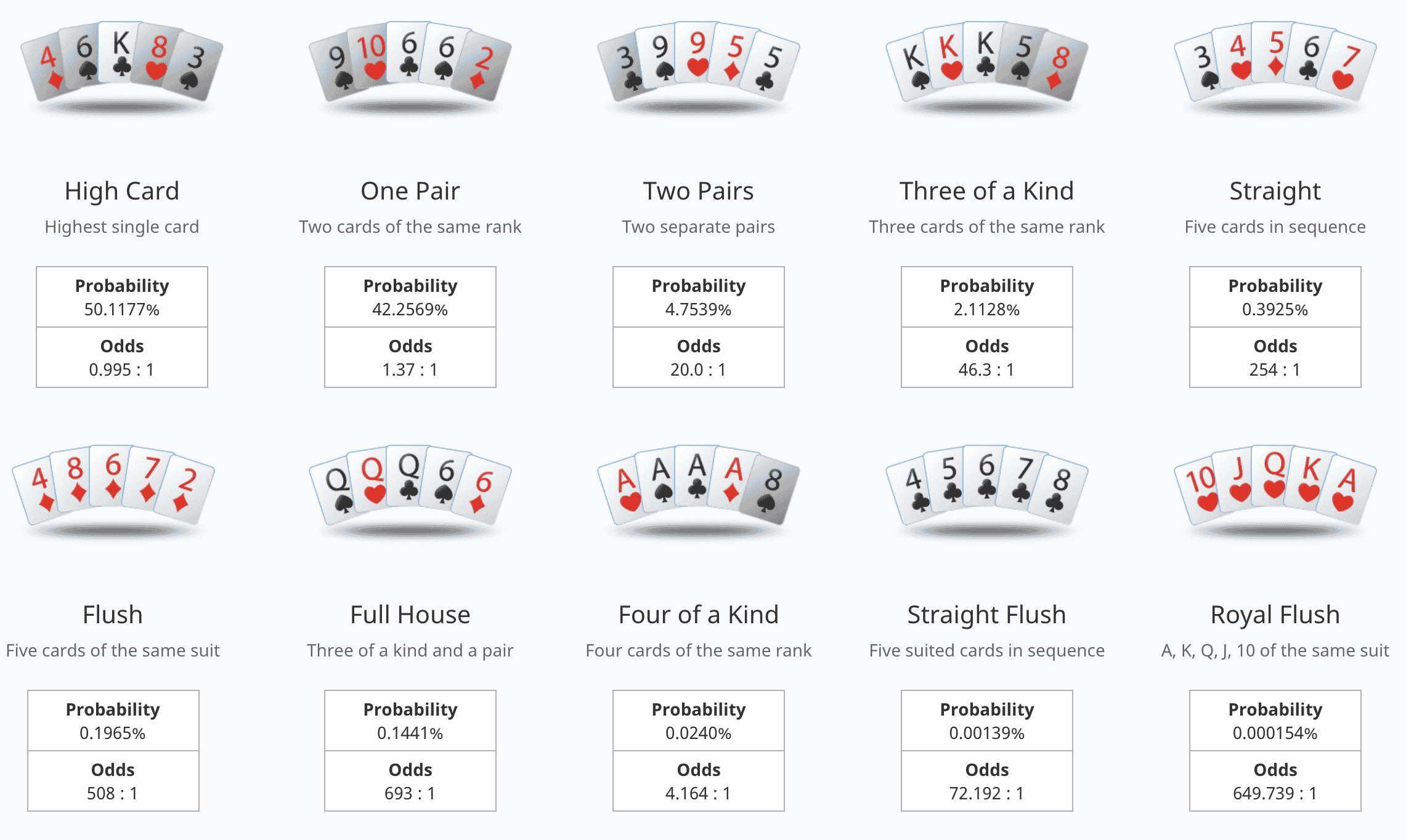
Probability Theory Probability

This is a problem concerning basic probability calculations from the text: “A First Course in Probability Theory” by Sheldon Ross (8th addition).

Sample Problem

Chapter 2 #16. Poker dice is played by simultaneously rolling 5 dice. Show that:
a) P[no two alike] = .0926, b) P[one pair] = .4630, c) P[two pair] = .2315, d) P[three alike] = .1543, e) P[full house] = .0386, f) P[four alike] = .0193, g) P[5 alike]=.0008.

Solution

Notation, I will let ^ designate the power function. For example, 6^5 is 6 to the fifth power. 6! is 6 factorial, 6! = 6 * 5 * 4 * 3 * 2 * 1.
To calculate the Probabilities here, we will divide the number of occurrences for a particular event by the total possibilities in rolling 5 dice.
N[total] = total possibilities in rolling five dice = 6^5 = 7776
Note: N[total] is the number of ordered rolls. For example, if we rolled the dice one by one and rolled in order 3,4,5,6,2, it would be considered as different from if we rolled 2,3,4,5,6 in order.
a) P[no two alike]
There are 6 choices of numbers for the first dice. The 2nd dice must be one of the remaining 5 unchosen numbers, and the 3rd dice one of the 4 remaining unchosen numbers, and so on… This gives an ordered count, so:
N[no two alike] = 6 * 5 * 4 * 3 * 2 = 720
P[no two alike] = N[no two alike]/N[total] = 720/7776 = 0.09259259
b) P[one pair]
First we count the possible sets (unordered) of numbers. Here we have one number that is the pair, 6 choices. Then we must choose 3 different numbers from the remaining 5 values, as these three are equivalent, we have choose(5,3) = 5!/(3! * 2!) possibilities. So 6 * choose(5,3) is the total combinations of numbers. Since we are dealing with ordered counts, we must consider the orderings for each set of numbers. We have 5 die with 2 the same so the number of orderings is 5!/2!. Multiplying these together gives us the number of ordered samples:
N[one pair] = 6 * (5!/(3! * 2!)) * (5!/2) = 3600
P[one pair] = N[one pair]/N[total] = 0.462963
c) P[two pair]
Here we have 2 pairs which are equivalent, so we must choose 2 values from the 6 possible values, choose(6,2)= 6!/(2! * 4!). Then we must choose 1 value from the remaining 4 for the single value, 4 ways. Now we must consider the orderings, 5 die with 2 sets of 2 the same so the number of orderings is 5!/(2! * 2!).
N[two pairs] = (6!/(2! * 4!)) * 4 * (5!/(2! * 2!)) = 1800
P[two pairs] = N[two pairs]/N[total] = 0.2314815
d) P[three alike] (the remaining two cards are different)
There are 6 choices for the three of a kind. Then we must choose 2 different values from the remaining 5 choices, choose(5,2) = 5!/(2! * 3!). The number of orderings is 5 items with 3 being identical, which is 5!/3!.
N[three alike] = 6 * (5!/(3! * 2!)) * (5!/3!) = 1200
P[three alike] = N[three alike]/N[total] = 0.154321
e) P[full house] 3 alike with a pair.
We need one value for the three that are alike, 6 ways, and then we must choose from the remaining 5 values for the pair, 5 ways. The orderings are given by 5!/(3! * 2!).
N[full house] = 6 * 5 * (5!/(3! * 2!)) = 300
P[full house] = N[full house]/N[total] = 0.03858025
f) P[four alike]
We need one value for the four of a kind, and then one value from the remaining 5 for the last die. The number of orderings is given by 5!/4!.
N[four alike] = 6 * 5 * (5!/4!) = 150
P[four alike] = N[four alike]/N[total] = 0.01929012
g) P[five alike]
Here we need 1 value for the five alike, 6 ways. There is just 1 possible ordering as all five die are the same.
N[five alike] = 6
P[five alike] = N[five alike]/N[total] = 0.0007716049
Check: the numbers of each type must sum to N[total] = 7776:
720 + 3600 + 1800 + 1200 + 300 + 150 + 6 = 7776

Probability Theory Predicts That There Is

Extra:
Straight
We can have two possible straights: one composed of (6,5,4,3,2) and one composed of (5,4,3,2,1). Each of these straights can be permuted 5! ways.
N[straight] = 2 * 5! = 240
P[straight] = N[straight]/N[total] = 0.0308642

Now let’s run a simulation in R:

Results of simulation:
notwoalike: 0.09194
onepair: 0.464
twopair: 0.23187
threealike: 0.1554
fullhouse: 0.03727
fouralike: 0.01889
fivealike: 0.00063
straight: 0.03072

Probability Theory Power System Reliability